Unit 10 Polynomial and Rational Functions Review Answers

three.R: Polynomial and Rational Functions(Review)

1. Concluding updated

2. Save equally PDF

Page ID

19674

3.1 Complex Numbers

Perform the indicated functioning with circuitous numbers.

1) \((4+3 i)+(-ii-5 i)\)

Respond

\(two-2 i\)

two) \((6-five i)-(ten+3 i)\)

3) \((2-3 i)(three+6 i)\)

Answer

\(24+3 i\)

4) \(\dfrac{two-i}{2+i}\)

Solve the following equations over the complex number arrangement.

five) \(x^{2}-4 x+v=0\)

Reply

\(\{2+i, 2-i\}\)

6) \(x^{ii}+2 x+10=0\)

three.2 Quadratic Functions

For the exercises 1-2, write the quadratic office in standard form. Then, requite the vertex and axes intercepts. Finally, graph the function.

1) \(f(ten)=x^{2}-4 x-5\)

Answer

\(f(x)=(x-2)^{2}-9\) vertex \((2,-ix)\), intercepts \((5,0); (-one,0); (0,-5)\)

2) \(f(x)=-2 x^{2}-4 x\)

For the bug 3-4, find the equation of the quadratic function using the given information.

three) The vertex is \((-2,3)\) and a point on the graph is \((three,six)\).

Answer

\(f(x)=\dfrac{3}{25}(ten+two)^{2}+3\)

iv) The vertex is \((-3,half dozen.five)\) and a indicate on the graph is \((two,6)\).

Answer the following questions.

5) A rectangular plot of land is to be enclosed by fencing. 1 side is forth a river and so needs no fence. If the full fencing available is \(600\) meters, find the dimensions of the plot to take maximum area.

Answer

\(300\) meters by \(150\) meters, the longer side parallel to river.

vi) An object projected from the ground at a \(45\) caste angle with initial velocity of \(120\) feet per 2d has height, \(h\), in terms of horizontal distance traveled, \(x\), $$given by \(h(ten)=\dfrac{-32}{(120)^{2}} x^{2}+x\). Observe the maximum elevation the object attains.

iii.3 Ability Functions and Polynomial Functions

For the exercises 1-3, determine if the office is a polynomial role and, if so, give the degree and leading coefficient.

1) \(f(10)=iv x^{5}-3 x^{3}+2 x-ane\)

Answer

Aye, \(\text{degree} = 5\), \(\text{leading coefficient} = iv\)

two) \(f(x)=5^{x+ane}-x^{2}\)

three) \(f(ten)=x^{2}\left(3-6 10+x^{ii}\right)\)

Reply

Yes, \(\text{degree} = iv\), \(\text{leading coefficient} = 1\)

For the exercises 4-6, determine end beliefs of the polynomial office.

iv) \(f(x)=2 x^{4}+3 x^{iii}-5 x^{2}+seven\)

v) \(f(x)=4 x^{iii}-half dozen x^{two}+2\)

Answer

Every bit \(x \rightarrow-\infty, f(x) \rightarrow-\infty \), equally \(x \rightarrow \infty, f(x) \rightarrow \infty\)

6) \(f(x)=two 10^{ii}\left(1+3 ten-x^{2}\right)\)

3.four Graphs of Polynomial Functions

For the exercises 1-three, find all zeros of the polynomial part, noting multiplicities.

1) \(f(x)=(ten+three)^{2}(2 x-1)(x+1)^{3}\)

Answer

\(-3\) with multiplicity \(ii\), \(-\dfrac{1}{2}\) with multiplicity \(1\), \(-1\) with multiplicity \(3\)

2) \(f(x)=x^{five}+4 x^{four}+4 x^{3}\)

3) \(f(x)=x^{3}-4 x^{2}+x-4\)

Reply

\(4\) with multiplicity \(one\)

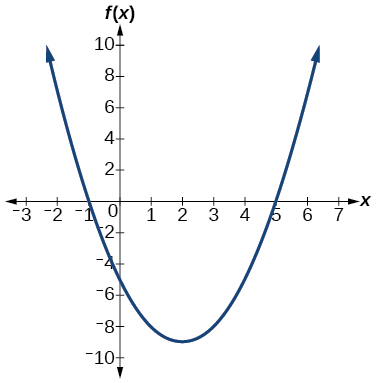
For the exercises iv-5, based on the given graph, make up one's mind the zeros of the role and note multiplicity.

iv)

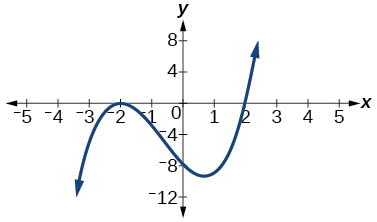
v)

Answer

\(\dfrac{i}{two}\) with multiplicity \(1\), \(3\) with multiplicity \(iii\)

6) Use the Intermediate Value Theorem to bear witness that at least one zero lies between \(2\) and \(3\) for the part \(f(x)=ten^{3}-five ten+1\)

3.5 Dividing Polynomials

For the exercises 1-2, employ long segmentation to find the quotient and residuum.

1) \(\dfrac{x^{3}-2 x^{two}+four x+four}{x-2}\)

Answer

\(10^{ii}+4\) with balance \(12\)

2) \(\dfrac{3 x^{4}-iv x^{2}+4 x+eight}{x+1}\)

For the exercises three-6, apply constructed partition to find the quotient. If the divisor is a factor, so write the factored form.

3) \(\dfrac{x^{2}-2 x^{two}+5 10-1}{ten+three}\)

Answer

\(x^{two}-5 ten+20-\dfrac{61}{ten+3}\)

four) \(\dfrac{10^{two}+iv x+x}{x-iii}\)

5) \(\dfrac{ii x^{three}+6 x^{2}-11 10-12}{ten+iv}\)

Answer

\(2 ten^{2}-2x-3\), and then factored form is \((ten+four)\left(2 x^{2}-2x-iii\correct)\)

6) \(\dfrac{3 ten^{four}+3 x^{3}+2 10+2}{10+1}\)

3.half dozen Zeros of Polynomial Functions

For the exercises 1-4, use the Rational Nil Theorem to help you solve the polynomial equation.

i) \(ii x^{three}-3 x^{2}-eighteen x-8=0\)

Answer

\(\left\{-2,4,-\dfrac{i}{2}\right\}\)

ii) \(3x^{3}+11 10^{2}+8 x-four=0\)

3) \(2 ten^{4}-17 x^{3}+46 x^{2}-43 x+12=0\)

Answer

\(\left\{1,3,four, \dfrac{1}{two}\right\}\)

four) \(4 x^{4}+8 x^{3}+19 10^{2}+32 x+12=0\)

For the exercises five-6, use Descartes' Dominion of Signs to observe the possible number of positive and negative solutions.

five) \(ten^{3}-3 x^{ii}-ii x+iv=0\)

Answer

\(0\) or \(2\) positive, \(1\) negative

half dozen) \(2 ten^{4}-x^{3}+4 ten^{2}-5 x+1=0\)

3.7 Rational Functions

For the following rational functions 1-iv, find the intercepts and the vertical and horizontal asymptotes, and and then utilize them to sketch a graph.

ane) \(f(x)=\dfrac{ten+ii}{x-5}\)

Reply

Intercepts \((-2,0)\) and \(\left(0,-\dfrac{2}{5}\right)\), Asymptotes \(10=5\) and \(y=one\)

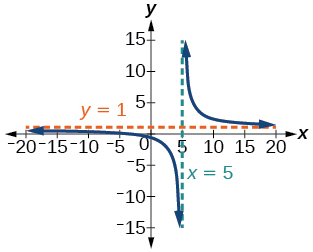
2) \(f(10)=\dfrac{x^{2}+1}{x^{2}-four}\)

three) \(f(10)=\dfrac{three x^{2}-27}{x^{two}-nine}\)

Answer

Intercepts \((3,0),(-3,0)\), and \(\left(0, \dfrac{27}{two}\right)\), Asymptotes \(x=1, x=-two, y=3\)

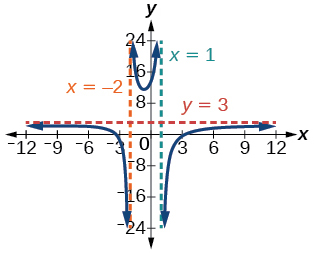
iv) \(f(x)=\dfrac{10+2}{x^{2}-9}\)

For the exercises 5-6, find the slant asymptote.

5) \(f(x)=\dfrac{x^{2}-1}{x+2}\)

Answer

\(y=x-2\)

vi) \(f(x)=\dfrac{2 ten^{3}-ten^{2}+4}{10^{2}+1}\)

iii.eight Inverses and Radical Functions

For the exercises 1-six, observe the inverse of the office with the domain given.

1) \(f(x)=(x-2)^{2}, x \geq 2\)

Answer

\(f^{-1}(x)=\sqrt{10}+2\)

2) \(f(10)=(10+four)^{2}-3, x \geq-iv\)

3) \(f(x)=x^{two}+6 x-2, ten \geq-3\)

Answer

\(f^{-1}(x)=\sqrt{ten+eleven}-3\)

four) \(f(ten)=2 x^{three}-3\)

5) \(f(x)=\sqrt{four x+5}-three\)

Answer

\(f^{-1}(x)=\dfrac{(10+iii)^{2}-v}{four}, 10 \geq-3\)

6) \(f(ten)=\dfrac{ten-3}{2 x+ane}\)

iii.9 Modeling Using Variation

For the exercises ane-iv, find the unknown value.

1) \(y\) varies direct as the square of \(x\). If when \(x=3, y=36\), find \(y\) if \(x=4\).

Answer

\(y=64\)

ii)

warrinerwhover.blogspot.com

Source: https://math.libretexts.org/Bookshelves/Precalculus/Precalculus_%28OpenStax%29/03:_Polynomial_and_Rational_Functions/3.R:_Polynomial_and_Rational_Functions%28Review%29

Share this post